Green's Functions and the Heat Equation • Dom Sauta

The Heat Equation in one dimensional space is one of a handful of special partial differential equations that seem to pop up in a range of different applications within the mathematical physics, applied mathematics and finance disciplines respectively. In our case, it is defined as follows:

\frac{\partial u}{\partial t} = \alpha \frac{\partial^2 u}{\partial x^2}

With initial conditions $u(x,0) = f(x)$ .

Where $u(x,t)$ represents temperature, and $\alpha$ is a constant representing thermal diffusivity.

In this blog post, I am going to explore the Green’s Function solution to the Heat Equation.

The Dirac Delta Function

Before I introduce Green’s Function, it is important to have some background understanding of the Dirac Delta function. The Dirac Delta ( $\delta$ ) function is known as the unit pulse function. It can be defined as follows:

\delta(x - x_0) = \begin{cases} \infty \quad \, x = x_0 \\ 0 \quad \, x \neq x_0\\ \end{cases}

With the useful property that:

\int_{-\infty}^{\infty} \delta(x - x_0)dx = 1

You can think of the $\delta$ function as a single infinite pulse, with zero value elsewhere. It is also interesting to consider the $\delta$ function in terms of the limit as $\sigma$ tends to $0$ of the non-standard normal distribution. This gives more intuition as to why the above integral is equal to one:

\begin{aligned} \lim_{\sigma \to 0} \bigg[\frac{1}{\sqrt{2\pi \sigma^2}} e^{-\frac{(x-\mu)^2}{2\sigma^2}} \bigg] &= \begin{cases} +\infty \quad \, x = \mu \\ 0 \quad \, \text{otherwise} \\ \end{cases} \\[2em] &=\delta(x - \mu) \end{aligned}

With this knowledge, we are ready to explore Green’s Function.

Green’s Function

In general Green’s Functions can be thought of as integral kernels that are useful for solving partial differential equations initial value problems. In our context, our Green’s Function is a solution to the following:

\frac{\partial G}{\partial t} = \frac{1}{2}\sigma^2 \frac{\partial^2 G}{\partial x^2}

Subject to initial conditions: $G(x, 0) = \delta(x- x_0)$ .

Thinking in terms of the Physics application, we can consider this partial differential equation (PDE) as a way of modelling the diffusion of heat along a one-dimensional rod of arbitrary length in both directions. The closed system is initialized with a finite heat source of infinite temperature at point $x_0$ , which then diffuses outwards in both directions.

It is known that the following is a solution to the PDE and the corresponding Green’s Function for the problem at hand:

G(x,t; x_0) = \frac{1}{\sqrt{2\pi\sigma^2 t}}e^{-\frac{(x-x_0)^2}{2\sigma^2 t}}

Which is a non-standard normal distribution with mean $x_0$ and variance $\sigma^2 t$ . This makes sense, as when $t = 0$ , we arrive back at the $\delta$ function which, as time progresses, flattens out into a more platykurtic function. Let us construct a visual representation of the solution with the following function parameters:

sigma = 1
x0 = 0

curve(dnorm(x, x0, time), xlim=c(-4,4), ylim = c(0,2), bty = "L",
        col = "blue", xlab = 'Position (x)', ylab = 'Temperature (u)', lwd = 1.5)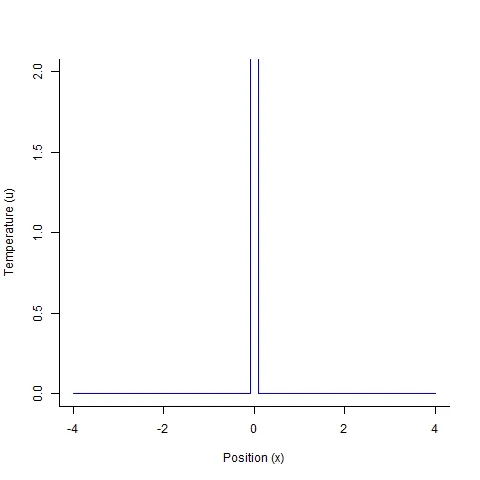

Notice the diffusion of heat from a centralised point at $x_0$ , to an almost uniform distribution as time progresses.

Generating Solutions to the PDE:

Green’s Functions becomes useful when we consider them as a tool to solve initial value problems. It can be shown that the solution to the heat equation initial value problem is equivalent to the following integral:

u(x,t) = \int_{-\infty}^\infty f(x_0)G(x,t;x_0)dx_0

Where $f(x)$ is the function defined at $t=0$ for our initial value problem.

We will make use of this property in a future post to solve the Black Scholes Heat Equation.